Software warranty with Java 8
 Can we give assurances that a piece of software will run virtually flawlessly for a period of time (say, one year)? Can we give timed warranties in software products, just as other engineering industries have been doing since the dawn of the industrial revolution?
Can we give assurances that a piece of software will run virtually flawlessly for a period of time (say, one year)? Can we give timed warranties in software products, just as other engineering industries have been doing since the dawn of the industrial revolution?
The question seems absurd because, unlike physical parts, software components don’t change with time. Yet, software performance does degrade with time (because its execution environment changes) and more often than not it is exactly time that makes difficult and nasty bugs surface, often with bad consequences.
In absolute sense, it is impossible to guarantee software. Software is way too complex and non-standard to sustain rigorous and legally-binding warranties, let alone that bug-free software is not only a practical impossibility but also a mathematical absurdity1).
Yet, given the right testing methodologies, it is possible to say with enough confidence that a certain software component will run virtually flawlessly for a period of time, under specified conditions. The bugs will be there, some of them will even manifest during the warranty period, but they will be few and far between and their effects will be under control.
I’ll show in this article how to do it, via a simple example. Disclaimer: the illustrative code below is in Java 8. Nevertheless, these principles apply to any language that is capable of generating values lazily - which extends the range to pretty much everything (given the right effort).
The Monte Carlo method
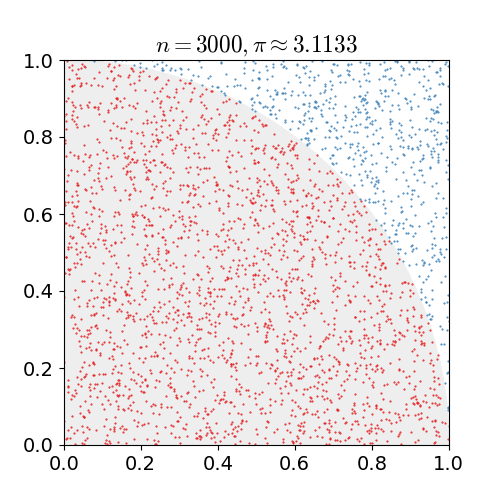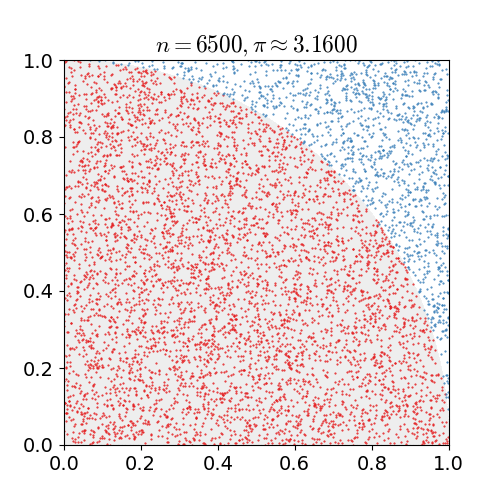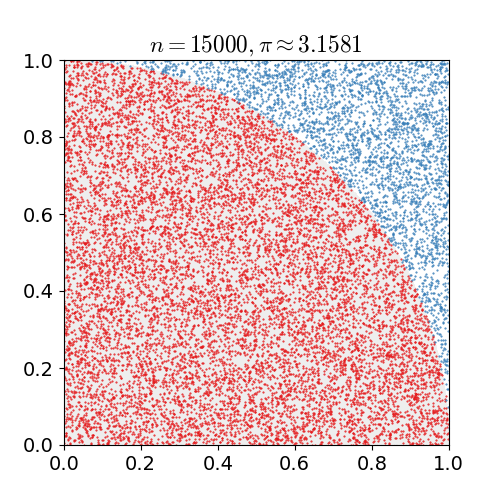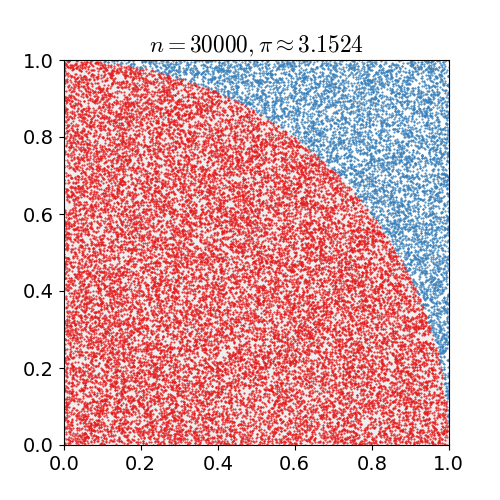 Assuming a piece of software is well tested (it functions as expected, it is backed by a solid battery of unit tests and it doesn’t have obvious flaws like resource leaks or inefficient algorithms) then its behaviour degrades not because of internal decay but because its execution environment changes and these changes have an impact with time.
Assuming a piece of software is well tested (it functions as expected, it is backed by a solid battery of unit tests and it doesn’t have obvious flaws like resource leaks or inefficient algorithms) then its behaviour degrades not because of internal decay but because its execution environment changes and these changes have an impact with time.
So, the first thing to do is to understand those environmental changes.
Understanding the environment
Environment can be modelled by constructing a N-dimensional space of environmental variables:
- inputs (shape, quantity, rate of invocations, etc)
- execution model (single threaded, multi-threaded, multi-process, distributed locally, distributed remotely, sand-boxed, etc)
- runtime conditions (OS, VM, browser, framework or library versions, accompanying software, etc)
- resource availability (memory, handles, connections, ports, etc)
- I/O (bandwidth, latency, failure rate, etc)
- … and so on.
For each environment variable it is necessary to build a set of possible values comprehensive enough to cover the situations that occur in practice. For most variables this set is very large or virtually infinite (take, for example, the total set of programs that we can feed to a compiler).
How many variables to add to that space? It depends on the case and choosing what to include and what not to include is always a trade-off between quality and practicality. But once that is done, the next thing is to understand time.
Understanding time
We cannot wait a year to see that our software will last that long, so we need a way to compress that period into something shorter. This is achieved by estimating the level of usage our software will undergo for one year.
For example, if we write a compiler for a new language and we distribute it to our friends, we can assume there will be only 20 people running it 3 days every month over the incoming year. This puts the total number of programs that our compiler will process to something around 20x12x3x10x60 which is less than 450,000 (this assumes a compilation every minute for 10 hours a day while the compiler is being used three days a month by its 20 users).
If we can generate quickly 450,000 programs, we’re quite safe to claim that our compiler will not disappoint our friends for one year. Generating 450,000 programs is not as difficult as it seems: we can generate 450,000 syntax trees and we can traverse each tree to generate the source code for it. The whole process is, in fact, a compilation in reverse, it probably takes just a few tens of minutes and it has to be done once.
Thus, we compress one year worth of compiler inputs in just a few tens of minutes of data generation.
Putting it all together
Once we have the domain of environmental variables and we have an understanding of the time dynamics of our software usage, we can proceed with our process:
- we sample the domain of our environmental variables under a distribution as uniform as possible (see below why)
- for each sample we put our software to work under the conditions dictated by the sample. OBS: this may not be possible to do automatically. For example, we cannot change the operating system at runtime.
- we stop when we reach the number of samples to cover one year of functioning (or whatever period we want to guarantee)
This way we simulate one year of functioning in a few hours (or days) of automated execution. If all that passes without errors, we’re quite safe to say that our software will run virtually flawlessly for one year of continuous functioning.
Generating the samples
 Let’s say that we want to guarantee that a processor of mathematical expressions will work virtually flawlessly for one year. Our processor needs to process abstract syntax trees representing the mathematical expressions. For simplicity, we represent these expressions according to the following grammar:
Let’s say that we want to guarantee that a processor of mathematical expressions will work virtually flawlessly for one year. Our processor needs to process abstract syntax trees representing the mathematical expressions. For simplicity, we represent these expressions according to the following grammar:
Expr –> Const | UnOp Expr | Expr BinOp Expr
Const –> Int | Float
UnOp –> ‘-‘
BinOp –> ‘+’|’-‘|’*’|’/’|’**’
The following classes will fit the bill (full code in the Appendix below):
- MathExpr has a property type of type Type which is an enumeration of CONST, UNARY, BINARY.
- UnOpExpr extends MathExpr and has two properties:
- operator of type String
- operand of type MathExpr
- BinOpExpr extends MathExpr and has three properties:
- operator of type String
- left operand of type MathExpr
- right operand of type MathExpr
- ValueExpr<T> extends MathExpr and has a property value of type T
The most important bit is the class that generates abstract syntax trees based on MathExpr and derived, in a controlled random manner. We call this class MathExprGenerator and we endow it with a random generator whose seed is given upon construction:
public class MathExprGenerator {
private final Random rnd;
public MathExprGenerator(int seed) {
rnd = new Random(seed);
}
// more code here ...
}
It is essential to provide a seed in all circumstances, otherwise the generated sequence will not be reproducible. We must have reproducibility when something goes wrong and we need to debug.
Generating integer values
Now we proceed with building up the generator. We achieve this by adding generating functions to MathExprGenerator. We’ll make use of the Enumerator class that I presented in a previous post.
Enumerator is nothing else than an Iterator enhanced with compose-able operations – much like .NET LINQ operators and Java 8 streams. Unlike Java 8 streams, though, Enumerator supports high compose-ability: it can undergo hundreds of thousands of concatenations, mappings or filter operations without overflowing the stack.
Let’s write the function that generates ValueExpr<Integer> instances:
public class MathExprGenerator {
private final Random rnd;
public MathExprGenerator(int seed) {
rnd = new Random(seed);
}
public Enumerator<ValueExpr<Integer>> integers() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextInt())));
}
// more code here ...
}
The integers() function simply converts a supplier of ValueExpr<Integer> instances into an enumerator. Using Optional<ValueExpr<Integer>> is necessary because Optional.empty() is the marker for when the enumerator ends (in this case, never). Using a dedicated randomizer for integers() is also necessary because the generators should be probabilistically independent of each other.
The essential thing to understand here is that no value is actually generated when integers() gets called. The function just returns an enumerator; the values will get generated lazily when the enumerator will be enumerated.
Generating float values
Generating ValueExpr<Float> follows the same pattern:
public class MathExprGenerator {
private final Random rnd;
public MathExprGenerator(int seed) {
rnd = new Random(seed);
}
public Enumerator<ValueExpr<Integer>> integers() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextInt())));
}
public Enumerator<ValueExpr<Float>> floats() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextFloat())));
}
// more code here ...
}
Generating constant values
Now that we can generate constant integer expressions and constant float expressions, we can generate constant numeric expressions by choosing either an integer expression or a float expression. We achieve this via a choice enumerator which takes two enumerators and builds a new one representing a choice between the two:
public class MathExprGenerator {
private final Random rnd;
public MathExprGenerator(int seed) {
rnd = new Random(seed);
}
public Enumerator<ValueExpr<Integer>> integers() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextInt())));
}
public Enumerator<ValueExpr<Float>> floats() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextFloat())));
}
public Enumerator<ValueExpr> constants() {
return Enumerator.choiceOf(firstInt(2),
nextInt(2),
integers().as(ValueExpr.class),
floats());
}
private IntSupplier firstInt(int bound) {
final Random rnd1 = new Random(rnd.nextLong());
return () -> rnd1.nextInt(bound);
}
private IntUnaryOperator nextInt(int bound) {
return x -> (x+1)%bound;
}
// more code here ...
}
The firstInt() function does the trick: it provides the index of the enumerator whose element will be picked next when constants() gets enumerated. Since the choice is controlled by the rnd field of MathExprGenerator, the choice is a fully controlled one, albeit random.
Generating random recursions
So far we have one generating function using two lesser generating functions: constants() uses integers() and floats() to generate constant expressions. This involves no recursion, so no extra care is needed in terms of laziness.
We have recursion when generating unary operator expressions and binary operator expressions; both unary and binary operator expressions depend on generic expression and generic expressions depend on both unary and binary expressions:
Expr –> Const | UnOp Expr | Expr BinOp Expr
This grammar snippet means that:
- A generic expression (Expr) depends on a constant expression (Const), a unary expression (UnOp Expr) or a binary expression (Expr BinOp Expr)
- A unary expression (UnOp Expr) depends on a generic expression (Expr)
- A binary expression (Expr BinOp Expr) depends on two generic expressions
This is translated into the following generating functions:
- Unary operator expressions get generated by a unOps() function returning an enumerator of UnOpExpr
- Binary operator expressions get generated by a binOps() function returning an enumerator of BinOpExpr
- Generic expressions get generated by an expressions() function that relies on constants(), unOps() and binOps()
- In their turn, both unOps() and binOps() rely on expressions()
- In order to avoid infinite recursions (and the associated stack overflows), unOps() and binOps() must call expressions() lazily
- The requirement of lazy calls does not apply to expressions(), which may call unOps() and binOps() eagerly
The following code speaks more than a thousand words:
public Enumerator<UnOpExpr> unOps() {
return Enumerator.of(this::unOperators)
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.map(p -> new UnOpExpr(p.getLeft(), p.getRight()));
}
public Enumerator<BinOpExpr> binOps() {
return Enumerator.of(this::binOperators)
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.map(p -> new BinOpExpr(p.getLeft().getLeft(),
p.getLeft().getRight(),
p.getRight()));
}
public Enumerator<MathExpr> expressions() {
return Enumerator.choiceOf(firstInt(3),
nextInt(3),
constants().as(MathExpr.class),
unOps(),
binOps());
}
The Enumerator.ofLazyIterator(this::expressions) construct embodies the above-mentioned lazy calls. This static method takes an Iterator<E> supplier and builds an enumerator which will invoke the supplier only when needed. Once triggered, the enumerator will do nothing else than returning the elements of the inner iterator. This way the calls to expressions() are guaranteed to be lazy.
One can easily see that unOps() makes use of unOperators() and binOps() uses binOperators():
private Enumerator<String> unOperators() {
return Enumerator.of(() -> Optional.of("-"));
}
private Enumerator<String> binOperators() {
final IntSupplier index = firstInt(binOperandList.length);
return Enumerator.of(() -> Optional.of(index.getAsInt()))
.map(i -> binOperandList[i]);
}
private static final String[] binOperandList = {
"+",
"-",
"*",
"/",
"**"
};
Limiting generation
All the generating functions from above yield an unlimited set of elements, expressions() included. We can use the generated values only if we limit their number. The following code limits the generated expressions to 20 and prints them one by one:
public class Main {
public static void main(String[] args) {
new MathExprGenerator(20150221).expressions()
.limit(20)
.forEach(Main::log);
}
private static void log(MathExpr expr) {
System.out.println((++index) + ") " + expr);
}
private static long index = 0;
}
If we run this code we get the following output (this assumes appropriate toString() functions, see Appendix for full code):
1) 0.12302077
2) 0.04271567*(-(0.81940556*0.5291456))
3) 817104225**((-(-(0.33097762-(((-((-(0.08633214/((0.5413032+(-(0.4350515+(-((-((317589320**(((-0.51310134)-0.08340657)-((-((-(-((-(-(-(-((-632129735+(-(-((-0.1089375)+(-(-((-555937305)-(-1778156055))))))))+(-((((0.87645334**(-722816560+0.63476014))**(((0.47925133+-2083250088)+326316536)*(-(-1011656250+(-((-((1078421136/(0.14880335*0.8200156))+((((0.18551683*0.46328604)*594441403)**(-1130707410*(-(-340626130))))**-770344324)))*0.30571634))))))*(-(((-(-(-(-2009782963))))-(-0.1522668))**(((0.9917727/(-(-544215676)))*(((1770269914+0.8733592)-(-(((-2135654715-(-448557993))**(-158818487))-(-434678438))))+(0.13288462/(-0.98800015))))/(-((-2076002068)*(-(-(-(-(-(-((0.015899718/(-214021880))+-1959083075)))))))))))))**(-(-(-635454679))))))))))**(-(-(-(-0.21596497)))))))*0.87531525))+0.60982776)))/(-(-1066112483))))**(-1612208625/(((-(((-(-0.3659082))+0.9499086)+(0.65491086**(-0.9408111))))*(0.48528093*1788954548))+((-(((-(-0.0022328496))/(-0.7896778))+((-1571127467)-((((0.7342297*((0.6792023**(422464841/((-(-(-(-((-(-1934934869-(-(-18951498**(((-(-17522070+(-(-2004189016))))/0.69558924)**(-((((0.49508137/((((-0.77374846)-((0.4576732/(-(-1711893895**((-(-(0.60782075/(((-0.42518473)/(0.4479888**785601421))-(-325070668-(-1856458779))))))**(0.7057189**0.87234545)))))+(-(-(-1858073682)))))-((-0.17762768)+((554709722-0.6488043)**(-(-1140144561)))))**0.1816563))-((0.77644956/0.7907419)-(-(-1380182071+0.38843882))))*(-((-(-(-0.3996374)))-(-446118578))))-(-0.298742))))))))/(-((-(-((-((((-0.7339015)*((-177600895)**(-0.08795422)))+((-(-(0.042826414/195684709)))**(((-0.69950306)-0.2783515)*0.4662739)))-(-((-(-1612785241))/0.649504))))-((-((-551026974/(-(1459288290-(0.99612737*((-0.41693628)*0.9543548)))))-(-1162046562)))+((-(-((390758848-0.61421365)/(-1156921512))))**(-844550987/(((((-(-937645656+646586587))*(-0.8593529))*(-2040411453))+((-503494485**(((0.31114572**309752271)/(-64974104))*(-((0.8785699+(0.46942616+(-0.3864941)))-1183819917))))*((((-(-(-(-2142949189))))-(1043084836*((-(-(-(-130757180))))-(-(-(((-(((-((-1919145867)+(0.6615095*(((-(((-((((-((-(-1523480851*(-(810903027**1902210309))))*(((-((-((((-1236503262)+0.030163705)-(-2045464395))-0.33336657))-(-(-75160407))))**(-(2118452806+1747017054)))*((((0.9112641*399881859)*1778154559)/(-(-914058527)))*(-((((-0.38004023)**0.54873246)+(-(-(-1772276638))))*0.6484614))))))/0.3343979)**((-((-1244596550)*((-0.525469)+(2110407416+1322212657))))/(-(-0.84797746))))**1287086526))**(-(-((-((0.025767982+(-1816136852*(-0.2628371)))*(-((-(-(-1533921506)))*-284290295))))**(-((0.8622792-(-(-1404123524)))/-1021378997))))))*(693894891-690556112)))+(-(0.07586813/0.5106498)))+((((-(((-(-546565469))*(-(0.02981639**(1405341327*(0.9544237+(((-(-((1493564286/0.5382808)**0.41664964)))/0.9154215)*1130199648))))))**0.68706214))+(-((885400756-(-2057151952))*(0.65818065/0.5242937))))**-72477136)+((-((-1925871346)/0.055523455))/(0.4904858/0.050924122)))))))-((-((-1100203178**(-0.64095664))+((-(-((-964016864+0.6178653)**(-(-((-(-0.7149976))+-1372008560))))))+0.23842394)))+(-1913921461)))/1044630042))-0.7228309)*((-0.34300727)*((-1443433207+(-(-897033947)))-0.37150526))))))))*0.6082126)/(-((-399906755)/((-(-0.17180157))-((-(-(-(-(-((-(-(-(-1823319509))))-(0.3094514**(-(-1124751456)))))))))+0.23656058)))))))**((-(((-0.34628075)-(-855171536))-(-509387039-(-269282138))))**((((-(-((((0.6110068-1718541010)+(((-(-352127433))/(((((-(-0.6686638))**0.7763571)+((1611588150/((-(-(-(((-((((0.9199284*0.12881058)*(0.6787282**(-(-0.561245))))/1554643518)-0.51246244))/-1549966795)-(((((-0.36182076)-(-((-((-1335874187)*944428594))-((-178474194)/0.7083625))))**-1996681306)+0.58402383)-(-1858762453))))))/(0.9244725-(-1565372497))))+-500148105))*(-574650152))+((-(-(0.24410307*((-(-(-(-((-(-(-0.3089841)))-(0.8439347+608827357))))))*(-((-0.67863053)*(-0.9860834)))))))-(44106589-0.12234259))))*(((-0.84036094)+((((0.42724586/-2095863901)-(-1832974324+0.90793407))**(-(-((-0.879275)-(-(((-(-(((145565411*(-0.8720256))+((-(-(0.3587531-((((-(-0.80769247))/134879073)+((-0.14758998)-((-(-(-(-(-(((-((((0.47421658**(-(-(-0.26719344))))-(-495561760))-(79382683+(-437786996**0.39204252)))-(-821135957)))*(-(-2143109294)))*1562676892))))))/(-(-1829692706**(((-(-(-(((0.75072813**(-0.42025846))*(-(-(-(0.13678885*0.28846508)))))/0.6337712))))-(((-0.083145976)**(-(-(((-((-(290980957-(-1239942290)))-((-0.44840991)-0.78581166)))/2057820448)*(-1817655397-(-(-(-0.52170986))))))))*163890513))*(-0.3790031)))))))/(-0.9024603)))))*0.30418956))+(((-0.3566627)*(-1981334091))**0.37392306))))*(-(-((-((-(-1256440587))**-2014849554))-(-((-(-0.73984796))/0.8140767))))))-((-(((-(-1654515387))*((((-(-(-(0.39288753+(-(-(-(-0.5742991))))))))**(-0.19589692))-(-400354814*-35184959))*0.28543633))*(-(-0.84589547))))*-1276528671)))))))**-545019693))/((-((-(-((0.70452166**((0.92443144-((((-(0.45732528+1529127309))**1780633702)+((1700849846*(-419570161))-((((146645502*((((-(-1988109199))-(-(((-(-0.21657199))-(-(-(-0.7031448))))+290274347)))-0.29682273)-0.27440423))-(2065663278**(-1051123235)))-((-(-(-((-642984016)+1931893836))))*((-0.7419426)**0.25609082)))**(0.2338478**(-(-1129602295/(-(-2113051794))))))))/((-(0.1450029+(-(-(((-(((-627531454)**((-(-0.12297809))-(-746709719)))/(861656201/(((-((-(-0.91355085))+(-0.2847615)))*(-(-1275566567)))*(((-355552540**0.6419937)+0.6182476)**(-0.91602427))))))*1196607138)**(-(0.8615277*(((0.17399204+0.21999049)*(-(0.07298714*0.94510204)))+93596925))))))))/(-(-((-(-1843210684))+-438912933))))))+((-(-255921152))-1683501016)))*2063724358)))**(-(2051266995/(-0.033258438)))))**1304948344))))*(-((-(-(-0.03183651)))+((-((-((-(-(-(-(-(-0.15997285))))))**((((-(-0.4717877))/((((0.22223473+(((-((-(-(-((-0.7069429)**((-(-(1556527156*((-(-0.2107569))*0.165766))))*(-((((1761730579**((-0.7168658)**0.80579704))**(831602383**((512520130+((-(((1764676104+0.22076654)/((-0.00593549)**((-(-170189587))*0.5987647)))-0.6540619))*(-1383827540/(0.47074038*-84117865))))+-880456472)))-(-(-(((-(-20431153))/(-(((-0.051806867)+(-(((-0.41976452)+(-(((-(-(-1036158586)))-((-(((-(0.6803472-(-((-0.4226392)-((715205045**(-(-2111777941)))*(-(-(-(((-587894225)*(-1563870831*0.011750877))*(-0.5962368))))))))))-0.7714308)+(-(-(-((-1004544746-745253914)*0.5727859))))))-((-1776010633)/0.44285947)))/0.36421293)))+-1855866232)))*(-(-0.61381483)))))**0.9917436))))*(-((-0.52336043)/-2137866787)))))))))+(0.2822584*((-235677637+(-1620855294))**(((-((0.44576675/(((-(-2041965535))/(-(-1839555365)))-(-1437031036)))/(((((-(-695427763))*((((1764557673**((-0.53799886)+(-((((0.091546476-(-428275249))-(-(((0.2099281*0.41057068)-(-90791657))+(-(-(0.62539065*-2034550033))))))/6555815)/886544963))))+(((-(0.26146632**-1554058762))/(-(-(-(-(-(-1693567160)))))))/((-0.623701)+(-((-(-1104306194**(420163704-911296451)))-(-0.2543835))))))**-483966732)*((-((((((-(202742711/361701620))/-130937465)-((-(-(-(0.17141283-(125296667-(-250025540/1215195520))))))*2109631082))/((0.2458241/((-(-1280721979))/1571015263))/(-(-1352425502/((-(-(-(((-(-1197377618))*((((-(-((-(1606960211/(-807100794**(-0.8547321))))**(-(((((-(-(-0.13737583)))-(-(-(-(-1728554355)))))-(-(-(-(-(-0.5675967))))))+((-(0.78901035/(-(-((-207084506/(-(-((-1437563824/(-(-(-1362384817))))*(-(0.93925*((-(-490172985))*((-(-(((-((-(-0.9918585))+-1275023088))*(-1002298778+(-(-(-198067641)))))*(0.958102**0.013981104))))*(-(-(-(0.91015273/(-(-((-((((0.6374175-(-(((-0.043198228)*(-(-1786103433)))-(-0.1839388))))-2076148568)*0.96034545)/(-(-1751879991))))-(-(-0.30008805)))))))))))))))))**(-(-(-(0.91844666+(-((0.32874453**((-(-(((-470438595/(1948374615+111675252))*(-272292517-(-595374421)))-(((-1562070809/0.9295762)*((0.282129**(((-(-492923696))/1804440240)**((-(-185147313))*((-0.7915937)+((-(699750692*0.14310837))/0.023171484)))))+(-(-1911227190))))+567204856))))-0.49312806))/-1838032485)))))))))))+(-(-0.27432722))))+0.36241752)))))*1979547222)-(-2072939847))**(-(((((-(-((-((-(0.27434927+(-0.33462256)))+(-(1873543547**0.57113695))))+(-((0.73846/0.25992334)/1793621175)))))**(0.010039389**-1258793178))*0.60383666)**(-(-(-808706215))))-(-(0.29431975*-1284621291))))))/(1371437725-((((-(((0.74685407*(-((-((-(-(-301453111)))*-1776322158))-(874548592+(-1842071858+-254095848)))))*(-1885446523+0.54047334))-(168516875*-315306196)))**(-(-((-(-(-(-(0.34346592-(-229236003))))))/(-(-0.35751307))))))**((0.59753627*(-(-0.85633683)))**(-(-(-(-(-((((0.4694686**0.13764101)+1475505952)**(-0.63419443))**-125551753))))))))*(1958448127*(-(-2068312721*0.6649115)))))))))*-1830568396)))))*((-(-1378157623*497739394))/(-(0.95632267+(0.111754835*(0.56282187*((-(-454054193))+(-0.34495986))))))))-0.9166827))+((-0.3387915)-(-1076714766-(-(-(0.075786114*(0.22051388/242198770)))))))))-1041253781)/(-(-((((-((-198693749)**526843865))**((((-(-172635948))-979541526)*(-(-0.5507316)))-0.85081935))**(580542155+-1299045278))/0.49901742))))/(((-((-(-(-(0.1597256-((-1862688747)+(-(-997409234)))))))-0.6795205))*0.52482843)-(-0.35474646)))))+1643531539)**(-0.6823678))))))-0.9276726)/0.014032185))**(-(-0.6975869)))/-1343464898)*-693431723))-(-(927308623+((0.90272635**-1297884813)*0.6104477))))**((0.12869042**(-(-(-319721480))))+(0.028816104-(-(0.30893326+306359612)))))))/(-0.7440371)))/(-597215976/(-0.3023643))))))*(594876037**(-(-(-172806854)))))))-(0.046592057-(0.20517522+-1654626716)))/((((-1826238063**(((-(((-(-(-0.46277827)))-(((((((-((-(-(-((-(((-(-(-1825344203)))-(0.44968224**(((((-(-1378420057))**-1899647517)-628586281)/(-(-717992966)))**(-((0.7362112**(((-((0.3727516+(((((2007590011+(-917378546))-(-(-((((((0.08629513*(-(-1089816824)))*(-(-28840072*(-0.54290724))))**0.2043696)*(-0.16923892))**(-(-1200542359)))*(-(-(-916644130)))))))/((-((-0.45670974)+((-(-(0.5947637**-2016707575)))/((-1259247619**0.1946792)*2004996246))))/(-(-((-(-(-0.490722)))**(-(-(((1724820756**0.97881866)*(0.8402267/0.9208275))*(-794319020)))))))))+((-(211930268/(-(-425373161/(-(-((0.4358734/1232038152)/((-0.80583966)-(-(-0.12161368))))))))))+(-((-((-(-1509953213))+-1244577495))**(((813236750/(-1116804176))/(-1704844144**0.47010875))*(-(-1616825954/0.6426449)))))))**(-0.38479692)))-(-(-(0.8594949*(-1942956707))))))-(-((-1250552624**(-(-((-((((-(0.48600298**0.58610326))-0.5799264)**1001378217)**(((((-(-0.65930986))+(0.50608337-(-0.14661455)))+0.07290059)-((-(-862993867))/1746158224))-((-(-(-(-(-739231513)))))-416592309))))*989298690))))/0.063328266)))**(0.41538054**0.0022200942)))**1929821903)))))*-1833710767))*-1574103803))))/(-(-((((-(-921481643+(0.31152374+(-670604885))))*0.63998127)/(-(-(((((-((-((((1077696052-0.09721732)+(-(-345133562)))-0.6711208)**(166242339-((-(-(-(-1823622128))))*(-(-(-897714751)))))))-((-(-(-116711282*((-(((-(-((-(-1166777183))-0.6563399)))/(0.07225281*1268395092))*(-(-(((-0.3629499)-(-242552484))*1286975952)))))/((0.28181642+1933706983)/((-((-(-(-(-(-(0.16889626**(-(-0.88881266))))))))**0.072820246))/-1014409102))))))**0.794627)))-0.85796756)-((-((-(-0.49183965))-(((((-((0.9760708*(((-(-448551830))-0.9248163)-(-0.019743264)))**(-0.94505304)))*((-(-(-(-((-(0.08109331+(-1917818931)))+(-0.4302172))))))/(((-(((-0.29144108)/((((((0.65437293**-1622427622)/(1632113530/-784545866))-(((((-(-((((-(0.43890744+(-0.27362144)))+(-770323095/(-(-(-1251491333*0.5522271)))))/1351766307)*41856142)))+(-1797935714))-((-0.80148214)-(-(-(-(-((-0.16693097)+(((-((0.21088064**(-((-((-(((-(-(-2062165998)))+(-(-0.75650406)))+(0.40552914**(-1364023561/(-183409460-479491126)))))**(-(-(-(-(-0.79711705)))))))-((((-((-((((-(((((-(-0.98572034))*(((-0.7033886)+1760606016)*-1963738141))+(0.10405654+0.73907083))+((-((-((-0.15859413)+414838347))+1702080962))-0.48643798))-0.69322884))**0.1208657)+((-(-180298740+(-(-471891599))))+0.4968074))-(-790392250*(0.27010685*((-847257490)/(-(-210294441*1851924192)))))))**(-(-(-89986495)))))-(-2084588887))**((-(((-(-1496195744))/((1324618483+(-0.13166225))**0.035098314))+0.6055813))+0.53459936))-0.097284675))))**(-0.45711356)))**(-(-781383355)))/((-((-0.18296349)+(-1504198430+((-2063282136)-(-673063684)))))/0.6353305)))))))))**-816292919)/0.8175043))*1618423768)*0.06180042)-853954700))-((0.4058742*1478964420)+1255612196)))-(-(-((-814483560-0.014094353)**(-(1274474294/(-((634023913+((887564406*(0.104504526**((-((-(-(-((-1608751007+(0.6734203*(-(-(-(-1955517586))))))/1549782589))))-(-(-(445163906/(645882282+0.65694475))))))-0.5909012)))*-1392628791))+(-((48226271+0.6974076)-((-((-((0.5898534**(-(-(0.5200862-(-((((-((0.19271809*((0.5043085-(-(-(-0.9915343))))+(((-(0.9904336-(((-(-475692502))*-1812321760)**(-(-(-(-(-78750919))))))))*2089938016)**0.128178)))-(-(-125980321*((0.4831651-(-(-((((-1064526551)**0.6392766)/((-1737105975**0.4581384)-(-(-(0.13915801-(-(-0.9572085)))))))**(-0.030837178)))))+415219116)))))*((-((-1543678868*(-1610436194-((-0.84481704)*((-(930827847/(0.47822982*0.22384357)))**((-(-1652619240))+-1994741926)))))*144284237))*(-((-(((0.018396914+0.4779796)-(-(-1704238476)))+(2098999845**0.46610403)))*(0.06356323/(-0.33462882))))))**(-(0.39868093**(-(-(-(-(0.09657043-((0.34250903*(378983563/1161403542))*(-(1639322240+(-0.9857099))))))))))))/(-((((-(-(0.4901141*(1857914321+((-(-((-(-(-1576871115)))+0.8205597)))-(-(-((-90208135)**-986154355))))))))*(-0.3285628))/(-((((((-((-1109156435/(-1905147643/(-1390189999-(0.80020905+(-(-(180194920**0.65697587)))))))**((-(-838996719))**((-(((-(-1151175190))-(-(-(-1338373579+0.37969375))))/((-((-(-1397279727))-1299922250))-((-((-(-(-1487501435)))-((-(0.055855274-825143930))+(-(-(-472576755))))))/-1138550742))))-((-(-1611133380))+-1913364259)))))**1956112466)-(0.5631535**((-(-(-(-((-(-(-((-(-(-(-(0.7525291**1293065852)))))/((-(-0.8180057))**((-((-1630937202**0.6337091)**(-0.15951312)))*1091665515))))))/-1560164255)))))+-1643867096)))+0.22642213)*(663788104**(-(-(0.81886226-(-0.6235196))))))**(-((37759631/(-0.91302997))*0.5386646)))))+387026424))))))))/413572511))*(-(-1214998345))))**(-(-1071974153)))))))))))))**((-((-(-(((-((1915892795/0.59965396)-(((((-(-((-(-(-(-1187667763))))*(1397155547/-997992870))))*-234811673)**(0.03517741*(-(-0.8793012))))+0.9334226)/(((-1260753704*1316261071)*-378300751)/(0.13670391-(-(0.11674249**(-0.9516297))))))))*(-(-(-2004235543))))*0.87257844)))*(-(-(-(-(-(-834652518*0.22389483))))))))*(-(-(((-((-0.40612257)**0.095936716))/(-(-1444497025)))*(-(0.41433418+420525381)))))))))*(-(-(((-(-0.6640259))**0.5913463)-(-1808257919)))))-((-(-2110325914))*2060044264))-(-677041457))))+(-((-403815923/(-0.66821337))-149813422))))*397119496)**0.57399845))))*(0.8882196-(-(((-194292684)/(-0.31257558))+((-((-((-((-(-0.63727736))/0.20869172))**(-373938879)))-1575469355))-((-(-1302748827))**((-1838633920)/(-(-(((-(-(-806164372)))/((((((0.70884484**((-77257365-(-0.31566536))-0.020452559))**(-1322121231+(((((-((-(0.6484304/0.053553224))*(-(-(-1291458282)))))+((-(1484933486+0.40033263))-0.36637414))/(-(((-0.3888964)-(-0.17349982))*(-(-0.33004975)))))*(((-0.7214631)+0.6410222)*(-(-(-(-((748643093*(-0.36585933))-0.50455105)))))))**(-0.70195127))))+0.6017993)/(-(1274571952*0.53051114)))/2067256708)**(((-(-1925094287))/-1483700625)**(-0.10707617))))*(-(-(-((-1489916982-(-((0.35457957+(-0.7666498))+(-((-60426637)-(-824879684))))))*(-(((((-0.32840455)+(1489263389/(-1483281689-(((-(-(-1587000568**(-(-1408874755)))))+((0.7854041/(((0.6359334-((-(-360041337-(0.19479173/-860477650)))/(-(-(((-(-1808079035*(-851964513)))-(1362319216*(-0.016621351)))**((-0.69205457)-(-(-(-(1150723309/((-(-79356796))+0.2958575)))))))))))*(((0.431942**(-0.35770452))+(0.41224897/((-(-(1230676556/(-594888869/((-339576539)/(-(-((-(-(-(-630377978))))+(-(-0.6612364))))))))))+(-((812405062-(-(((-(-(-(-119303276))))/(-(((-(-(-383378226)))/(-((0.06553924-((-(-((((-(-(-152159961)))-(-(-(((-(-(-(0.09071541+(((-0.48533833)+((-0.9695876)+-1077073428))*-799008214)))))**(-(-499697915)))*0.48863465))))+(-(169257324-0.20261145)))*0.8586412)))/((-(-(0.02777195-(0.7745687/(-(-(-1277098483)))))))+0.7329658)))+(-(-0.032403767)))))+0.3968414)))*((-(-((-(-((-(0.97622085+((0.8923253-(-((-(-(-((-(-1124278507))*(-(0.66090274/((-(1691600033/0.025001228))/((0.056275785-(-((752144603**((-972710762**(-0.24726576))**0.19201648))*0.75559235)))**(-(-0.503614))))))))))+((0.5275381/0.42751437)-0.81197256))))+(0.9825565+(-0.76957583)))))/-1986359799)))/((((-((-347874155+(0.33329076-0.31708157))+0.4497772))*(139239542-((-(0.20938694*0.6604807))+((-1133641076-(-(-(-(-(-(0.8481999**(-(((-((-(-(-167654126)))/(-935485137/((0.9101935+(-573187976))**(-1980107974)))))-(-1329980975))*((-(-316741537))/((-((-(-2115093762))+-782911582))/0.074867964)))))))))))*749458156))))-(-1639010247))+(-(-2088407726-0.2060464))))))**(-0.87249494)))))*(-((-((-1426048655)*0.010127842))/(-0.1697579))))))))**0.9911719))**-2023886111))+(-329137747)))-0.4715166))))**(0.8258571+(0.95712316**0.25456876)))/-900073683)+-1642548534))))))))))))))))))))/((-2054596992*(-0.709506))*0.65047216))+(-816501209-(0.94132876+(-359542172-(-0.6719031)))))+-467869933)-0.20592111)/(-(-1403552062)))-(-521268253)))-(-(-(-(-(-1071316682)))))))**((-(-658602195))*699641730))**(-(-(0.96908826/(((0.90553284-0.18225104)/(-(-0.22723484)))-(-(((((-(1133861803+((0.8637799*0.7934642)-(-505690963))))+(-(-(-0.3434847))))+0.026126444)-(-0.594156))*(1066316794/526646471)))))))))+(-(((829634472*((-((-1035862679)/(-(-(-1381529146)))))*(((-(-1165722012))**((-6.748438E-4)**0.17271179))*((-(-0.6601027))*((-(-0.88684934))-1008803259)))))+-305036289)+0.6818751)))-((-(-722493159))/0.8627427))+((-0.49965805)+(-(((-1207029772)**(-((-0.78923124)-((-0.301211)**(-2078634642**(-(-1818871176/(1960107412*(-1476118766**0.69248486)))))))))*((-(((0.45090228**((((-((-((-(-(-360616415)))*(-0.26713115)))/(-(-0.55547833))))**-2013676541)-(0.66459024+(-(-0.25296545))))*(0.76872796**(-1868729407-(-(-1478366312**(-1261160446**(-(-((0.8370416+(-(-764438828)))*(((0.4007491+(((-0.42412525)/((-((-(-0.32816684))**(-(-((((-((-0.8955619)/(-0.3875456)))/(-(((-(-((-((((-(-(0.24967194/0.8028868)))*0.6636469)-831514659)/(-(-(-(-(-((((-(-(-0.030966401)))*-359762724)/(-(-((-(-((-0.25109375)/0.8785807)))+(-0.29145926)))))-(-(1191691824*-2134979803))))))))))-((-1198653808)-(-2031604132)))))+(0.71051896/-1615264180))**((-(-2104405876))-(-((2137757175*(-(-1606383758)))**(165225861/1834959174)))))))-(-(-(-(-((-(-0.24148315))**(-(-1397551145-1316044441))))))))*(-0.8463433))))))-(-((-1572455520)+765498139))))+(-((-(((-(-(-811239725)))+(-397309682**0.14310807))**642290204))-(-1386238440)))))*-17338764)+0.99241126)))))))))))**((0.105715275*2036344176)*(-1925626319*(-(-795221057)))))*(((((((((-(-(-315667644)))/(-(-(-(-1162591986/((((-2089977086**((-46629247-(((0.7050782*(-0.45932412))/((-(0.93069965+(1480922999+(-(0.4117673**(-(-(-(-0.20409656)))))))))+0.42460215))*967197454))**(-0.95025456)))-(-0.6688259))/(-((-0.43149316)**(-(630584364-(-0.18563831))))))**-215053946))))))+(-(-2086792410)))*((((0.3557254/-463397161)+(-(-0.040582776)))+-174807431)*(0.08680189+((-299085355)**(-(-(-(-135338320/(-0.18413031)))))))))**((-(-((-(((-(-(-(-(-(-1222629816+(1797109756*(-1692937268**(-(-128148257))))))))))*(0.69887996+(-125863937*(-(-(0.25533617*((((-(-1739168513))*(-1901301739+1256561679))-(-0.09665084))**-1887565008)))))))+(-0.7817246)))*((0.8821101*167812337)**(-(-(-(-0.97193885))))))))*(-(-((0.9362215**((((-212706276/0.40784204)-(-1089538173))-(-(-1800083491)))/((-(-(-((-(-1873207992))/0.7066315))))+((((-0.62007976)-0.30737275)/(-(-929431980*(-0.35274023))))/0.7769663))))**1883400478)))))**-64740903)+(0.4283586-(-(-682918236))))+(-776168274))*0.6511632)))*((1946262723**(1228339007-(-586828778)))*(1701874909/1180451793))))))))+(-(-((-((-(-(-(-(-484192105)))))**-1040991500))/((0.40710592-(0.31514335/(-(-(-0.3535176)))))+(-1216281971-(705620805-0.6163372)))))))))))))))**(-1763394749**(-((-1272400364/0.90004337)**0.6263401))))))))))*0.20699936)))/(((-2060015187)**((-(0.34700632-(-((-(0.7806879+0.19892824))+(-0.8207491)))))*((-(-((-(-(-((-(-(-((-931487714-2010147435)-((-(-2125939494-1115628698))**(0.76315653+0.08307123))))))**0.09987551))))*(-1796633395))))**(-1569415294))))**((0.5887767*0.07826537)-5261582))))-(-(-(1870709449*0.72567225))))-(-0.4017474))**0.61604446))))*(-(-(0.61356807-((((-(-(-(-(-0.8497051)))))**((-((-(-0.43792617))/((0.67937547/(-(-470125736*0.6057219)))/(-(-769920341)))))+(-(1459297077-(-(-(-(-(-((-((-0.5648522)/0.8898752))+(-((-(-(-(-(-1713252728)))))*0.55999464))))))))))))-((-((-((-(-(-991045291)))**0.1957035))+((1941593706*(265597756-(-(-0.38367313))))+0.6014179)))*(((-0.15239042)*-321889306)**1626021637)))*(-(-(-0.1381725)))))))))))))))+(-(0.0645231**-432126077)))))**((0.66651064/(((-691963013)+((-(0.66284466**(-(411892833-((-((-591953864+(-(-(-1136646253))))+(1061296082*(-(-1869585914)))))*(-0.6491834))))))**(-1399589292/(-(((((-(-(-(-((-((-0.34214956)-(-(-(-1819490117-(-1695395103))))))-0.3882596)))))+(-0.22477067))+0.4628473)-471559513)/(-1520904951))))))*((-(-1536175019))/0.6644887)))**-1032802905)))/1822226572)**(-2089712566/(-2017146303))))))-0.57705814)
4) 0.37527758
5) -0.32874078
6) -0.7665599
7) -(-(-(-2065855542)))
8) -(-237455063)
9) -(((-((-((((0.8511914*(-((765857203-(-(-0.11264199)))**(-1999017914-(-(-(-(-(-0.12968892)))))))))/(-971804282))**(-0.54657346))**(-(-(-1877231161+(-(-425938232**1049876691)))))))-(-655454968)))-(1912543806-(0.11868358+0.07560557)))/1130195601)
10) 0.5128824
11) -(-((1410472261/897107205)**((0.44386768+(((((-0.12256569)/(-(0.8154955+0.8856838)))/1367404253)+(-0.67957217))**((-(((-(-262187587))-0.39580476)*0.72937816))*(-0.36948055))))/(-((((-(-(-2072320263-((478918134-(((((-(0.10206944-((2032829797/(((-((-(-(-2120642602)))+(-(-0.6372956))))/((-(-0.08866829))+((-((((0.07008642-0.7487553)/((-(-(-1688734063)))-(-((-(-1509700405))*((-0.19771284)+0.57631385)))))+0.93647796)/1889227358))**1736289228)))**(-1643912481**(-((-((-(-(83298856**(-0.64789766))))/(-(((0.82620984*(-(-(-(-(-0.48842657))))))+0.09938961)-(-(-(-(-((-0.35980868)+(-((-0.14965093)*(-1949523782-(((-(((-0.5444034)/0.8561184)*(-255643747**(0.71956414*0.92949426))))+0.18755609)**0.15187544)))))))))))))**0.8909352)))))*((-0.6730308)/(((-1616734000)**(-(-1710475695)))/0.52109766)))))*((-((0.555339-(-(((-(-127556688))*(-(-1926627499)))+((-((-(-(-((-(565289603/0.9086512))**-1970064897))))/(591713500**0.66475767)))-0.18084592))))/((-((-0.7741902)**0.21543193))**0.54831797)))/(-(0.6362378+0.6997616))))/0.2589745)**((((-(0.48770916-0.36611325))+(-(-1113907832)))+(-199588254))**(-((-(0.7402031/(-0.6576252)))*(-(-(1964006618/((-((-(-((-(-(0.1841206+2136457193)))-(((-(-(0.87577474*(0.9031665**(-(-(((-((-(-(-(-(-(-1694389582))))))**(-((-(-153807167-(-(-1442004742))))/-950651738))))/(-(((-(-((0.69447404+0.60704625)**(0.3978585-(((-0.12274951)-(-(-(((-(-(-12739179)))+525972979)+(-(-((-91717787)**(-(-((-(-(-0.19205582)))/1405037258))))))))))**0.9460166)))))**((-((-1708747637-(((-(-(-(-(-(-((-(0.03869152+0.29090083))*(0.8515802+(-(-1915366392*(-1639772562)))))))))))/(((-(-(-(-((0.16152763*(-(1892761731+(-0.1327101))))+(-(-0.6824853)))))))-(-0.8624062))**0.5548538))+0.71153456))-521721572))+(-543840524+(0.289778**(-((-(-((1648909816*(2094976787**(-((-0.138125)*(1132703771*(-(-(-0.5197252))))))))+0.02198118)))+(0.31773394/((1008003032+0.25491822)+-200727599))))))))/(-0.49983567))))**(-(((-92327690)+0.46786684)+((0.18455482/(-((-((-1230328725)+((-((-0.18534756)**0.5404603))**0.7790049)))*(-0.39629823))))-(((-((-1354245150-1769747949)**-446059053))+(0.13886744+-1515952200))**(-(-(-516633783))))))))))))))**(-(-(0.6054196/1110619585))))/(1794407152+(0.76004153*(-(-131360050))))))))*(-(-((-(-0.939396))-(((0.15615767-(-483281613))/0.18192118)+0.7556193))))))*-2147362597))))))))-(-1976221711)))*(-(-(-(-1855741220))))))))*-42211259)+(((-0.6789443)-(-(-0.9949046)))/(0.19640422/0.5013496)))**(-((-1849266914**(-0.9574902))/(-1799377500-((-(-872007740))*-1972247068)))))))))
12) (-(-(((-((-(-1825433523))**1139047063))-0.5986636)*(-0.90291846))))*(-(-(-(-2025579308-(-((-(-(-(-(-(-((-0.8908368)+(-((-0.92736554)**0.24715143)))))))))+1568137377))))))
13) ((-358603623**0.30990857)-(-(-931612737)))*(-(-(1931927417-(-(-(-0.30606115))))))
14) 0.652911
15) -((0.035448253+(0.74276876/0.90598375))+0.7126012)
16) 506718243-((-(-(-0.47619313)))**0.099224985)
17) -(-(-438905441))
18) -((-(0.5024937-((0.3200944/(-((-(-(-(-(-830850136)))))**(-(-(((-(-(0.07288116/(-440890360/0.847317))))/(-(-(-(-((0.24419606**(-15754904))+-1508088305))))))*0.05566871))))))/0.84323686)))-684553608)
19) ((0.5417112/1278666327)*0.59889024)+(-((((-(-(((-1291494816)/(((0.2936504*0.6108249)/0.8510845)-(-623346138)))**0.2062015)))**(-(1786906146-(((0.60515976-((-(-((-0.54516053)+-222546669)))*(((-704787315-((-1524838499/0.3084811)/(-(0.5364434-(-(((-((-(-0.88833916))+-1380136643))+(-(-0.499902)))-(0.9759775**(-0.99971944))))))))+((-(-(874696286**(-(1687562973-(-0.559574))))))*(-(0.7774994+(-((0.85018986+0.31932408)-0.55392414))))))/(((-(((-(((-799935431)/1233505888)**(798471880/(((37095321-((-0.77204734)**(((-(0.47402984+(-1607833605)))*(-(-442957699)))+-1079969685)))/(((148469575/0.7748515)**((-(-((-1527527825)*(0.0992614/0.95039666))))*((-(-(-(-(1857949888-(-660840997**0.5921666))))))**(1706971334+0.88437194))))*-2076248651))+(-(-(-0.052259564)))))))**1054605989)**(-(-((1244189783-(-0.24012762))/(((-0.018929064)+(-(-2111173716)))-(-(-(-1557761016)))))))))/0.69783545)+226497202))))*(809107517+(-772212260/0.463378)))+(-((-0.22136849)**0.8606984))))))**(-(((-(-578436511))**0.20714217)-(-(-1908686340)))))+-722275261))
20) 0.48508495
Important: when we generate samples to guarantee our software, the number of expressions we want to generate isn’t arbitrary, it is dictated by the duration we want to guarantee our software for.
Thinking about depth
There is no limit in how deep the generated expressions will be. There is not much concern, though: with a 33% probability to degenerate into a constant, the average expression depth is 1+3 (root plus three levels of children).
This is just a probabilistic average. If we generate many expressions, the syntax tree may get 10 or more levels deep and may contain hundreds of thousands or even millions of nodes – which may be too much. The solution to this is to add depth limits to the functions of MathExprGenerator.
How to check it works all the way
Given that the number of samples is very large and unknown upfront, we cannot verify the outcome against a pre-defined set of values. Thus our checks must verify property invariants instead of actual values.
For example, if our expression processing algorithm evaluates the given expression, then:
- eval(e1 op e2) must equal eval(e1) op eval(e2) where op is any binary operator
- eval(e1 op e2) must equal eval(e2 op e1) where op is any commutative binary operator
- eval(u op e) must equal eval(e) where u is the neutral element for binary operator op
- eval(-e) must equal –eval(e)
- … and so on
Each check upon sample x turns into verifying a p(x) –> q(x) implication which passes when either p(x) is false or both p(x) and q(x) are true. Obviously, the actual check is q(x) so the sample set must have enough values that satisfy p. If that is not the case, then refining the sample generator may be in order.
Other samples
 In the above section I showed how to generate random inputs to such a degree of quantity and diversity that ensure virtually flawless execution for a year or more.
In the above section I showed how to generate random inputs to such a degree of quantity and diversity that ensure virtually flawless execution for a year or more.
This method of random sampling works not just for program inputs:
- The amount of available memory can be constrained at runtime, hence it is possible to generate stress-memory conditions on random basis
- The level of connectivity (size of connection pool, I/O latency) is also controllable at runtime (with some effort), allowing us to model random conditions in this respect
- The reliability of the I/O calls can also be altered at runtime:
- either by using sophisticated fault-injecting I/O drivers
- or by encapsulating the I/O calls into routines that support controlled random fault injection
- … and so on
Even though we cannot guarantee our software for every possible condition (a car maker doesn’t guarantee a car when used like a submarine), we can definitely offer software warranties under a specific set of conditions which we choose to satisfy.
The need for uniform distribution
 I stressed above that the samples should be picked up randomly according to a distribution as uniform as possible.
I stressed above that the samples should be picked up randomly according to a distribution as uniform as possible.
Why this requirement, knowing that the inputs and the environmental variables are far from being uniformly distributed? Is it realistic to test mathematical expressions of 10000 nested parentheses knowing that no-one will ever enclose this much?
The answer is yes, it is crucial that we distribute as uniformly as possible and if we don’t do it then we cannot give any timed warranty about our software.
To understand why uniform distribution is essential, let’s consider those hard software bugs that occur rarely (say, once a year or less) but when they occur, they usually have very bad consequences. Why are those bugs so hard to surface? Are they consciously hiding in the code? Is there some malevolent force baring us from getting to them?
Not at all. If you’ve ever dealt with such bugs then you know that the so-called hard bugs are often times quite trivial or even silly. Their rarity stems not from their “difficulty” but from the rarity of the conditions that make them manifest. By the same token, the toxic effect of “hard” bugs is not in their innate nature but in the unpreparedness of the system to face them, because of their rarity. Or, this rarity is the effect of the very large biases that dominate the universe of practical conditions.
So, if we follow such biases (even in the slightest) when we try to guarantee our software, then we’re doomed to failure: we’ll do nothing else than emulating the very same conditions that make the “hard” bugs hard in the first place. This will make our “warranties” practically worthless.
When ensuring for software warranties, we must not follow “normal” conditions of operations. Quite the contrary.
Ideally we should choose only those conditions that make the bugs manifest over the guaranteed period. But because we cannot know what those conditions are, choosing uniformly within the sample space will generate similar conditions which will possibly reveal other (but similar) bugs early on, thus forcing us to make our software truly robust and capable of handling even the most unexpected situations.
Conclusion
Software is hard and highly unpredictable. The enormous compose-ability of software constructs makes even average-sized programs to have state spaces so big that only astrophysicists might grasp. This, in conjunction with the highly fluctuant nature of our industry, makes legally-binding warranties a remote objective.
Yet, giving some degree of guarantees in software is not only possible, but also desirable. Arguably, many sleepless nights and hectolitres of coffee could have been spared if the software industry had attempted to match, even in a small measure, what our peers from other engineering disciplines have been doing for a very long time: taking the risk of saying “This will work as expected”.
1) It is impossible to have both “bug-free” and finite computational sequences into the same time.
We can intuitively reason the following way (this is not a rigorous proof): if we expect error X to occur, then our software must handle it (and possibly recover from it). Let’s say we insert code that handles X (for e.g. by logging inside a catch block). However, handling X (logging the error) may fail with error Y (for e.g. I/O exception). Error Y may be disruptive enough to require a special code to handle it (for e.g. close the log handle, remove some old logs, re-open and try again). But the piece of code handling error Y may throw error Z (I/O exception upon retrying because exactly in that moment some other process flushed a 3 GB buffer) and so on …
No matter how “careful” a piece of code is, it will always be liable to enter an error state from which it will not be able to recover gracefully. Hence, bug-free and finite code does not exist: handling properly every conceivable error will require an infinite number of error handling blocks.
In one hand, the “rock solid” code we find in real life is still buggy, but its bugs have such a low probability of occurring that, for all practical purposes, it is like bug-free.
On another hand, rigorous proofs that a piece of software is correct (by using formal methods, for example) rely on simplifying assumptions that do not hold under extreme practical conditions. The most notorious example is the assumption that we can always declare/allocate all the variables that we need (the “infinite memory” conundrum).
Appendix
This appendix contains the full source code of the examples herein.
MathExpr.java
package mathexpr;
public abstract class MathExpr {
public enum Type {
CONST,
UNARY,
BINARY
}
public final Type type;
protected MathExpr(Type type) {
this.type = type;
}
}
ValueExpr.java
package mathexpr;
public class ValueExpr<T> extends MathExpr {
public final T value;
public ValueExpr(T value) {
super(Type.CONST);
this.value = value;
}
@Override
public String toString() {
return value.toString();
}
}
UnOpExpr.java
package mathexpr;
public class UnOpExpr extends MathExpr {
public final String operator;
public final MathExpr operand;
public UnOpExpr(String operator, MathExpr operand) {
super(Type.UNARY);
this.operator = operator;
this.operand = operand;
}
@Override
public String toString() {
if (operand.type.equals(Type.CONST)) {
String img = operand.toString();
if (img.startsWith(operator)) {
img = "(" + img + ")";
}
return operator + img;
}
return operator + "(" + operand.toString() + ")";
}
}
BinOpExpr.java
package mathexpr;
public class BinOpExpr extends MathExpr {
public final String operator;
public final MathExpr left;
public final MathExpr right;
public BinOpExpr(String operator, MathExpr left, MathExpr right) {
super(Type.BINARY);
this.operator = operator;
this.left = left;
this.right = right;
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder()
.append(left.type.equals(Type.CONST) ? "" : "(")
.append(left.toString())
.append(left.type.equals(Type.CONST) ? "" : ")")
.append(operator);
builder = builder
.append(right.type.equals(Type.CONST)
&& !right.toString().startsWith(operator)
? "" : "(")
.append(right.toString())
.append(right.type.equals(Type.CONST)
&& !right.toString().startsWith(operator)
? "" : ")");
return builder.toString();
}
}
MathExprGenerator.java
package mathexpr;
import java.util.Random;
import enumj.Enumerator;
import java.util.Optional;
import java.util.function.IntSupplier;
import java.util.function.IntUnaryOperator;
public class MathExprGenerator {
private final Random rnd;
public MathExprGenerator(int seed) {
rnd = new Random(seed);
}
public Enumerator<ValueExpr<Integer>> integers() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextInt())));
}
public Enumerator<ValueExpr<Float>> floats() {
final Random rnd1 = new Random(rnd.nextLong());
return Enumerator.of(() -> Optional.of(new ValueExpr(rnd1.nextFloat())));
}
public Enumerator<ValueExpr> constants() {
return Enumerator.choiceOf(firstInt(2),
nextInt(2),
integers().as(ValueExpr.class),
floats());
}
private IntSupplier firstInt(int bound) {
final Random rnd1 = new Random(rnd.nextLong());
return () -> rnd1.nextInt(bound);
}
private IntUnaryOperator nextInt(int bound) {
return x -> (x+1)%bound;
}
public Enumerator<UnOpExpr> unOps() {
return Enumerator.of(this::unOperators)
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.map(p -> new UnOpExpr(p.getLeft(), p.getRight()));
}
private Enumerator<String> unOperators() {
return Enumerator.of(() -> Optional.of("-"));
}
public Enumerator<BinOpExpr> binOps() {
return Enumerator.of(this::binOperators)
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.zipBoth(Enumerator.ofLazyIterator(this::expressions))
.map(p -> new BinOpExpr(p.getLeft().getLeft(),
p.getLeft().getRight(),
p.getRight()));
}
private Enumerator<String> binOperators() {
final IntSupplier index = firstInt(binOperandList.length);
return Enumerator.of(() -> Optional.of(index.getAsInt()))
.map(i -> binOperandList[i]);
}
private static final String[] binOperandList = {
"+",
"-",
"*",
"/",
"**"
};
public Enumerator<MathExpr> expressions() {
return Enumerator.choiceOf(firstInt(3),
nextInt(3),
constants().as(MathExpr.class),
unOps(),
binOps());
}
}
Main.java
package mathexpr;
public class Main {
public static void main(String[] args) {
new MathExprGenerator(20150221).expressions()
.limit(20)
.forEach(Main::log);
}
private static void log(MathExpr expr) {
System.out.println((++index) + ") " + expr);
}
private static long index = 0;
}
Comments
Post a Comment